Pitágoras, mucho más que un teorema
La figura de Pitágoras
y los pitagóricos, han dado a las matemáticas mucho de qué hablar, debido a que
la historia nos muestra que gracias a su forma especial de entender el mundo se
lograron sentar las bases de la Geometría, la Aritmética, la Astronomía y la
Música. Dentro de sus principales aportes se destaca el Teorema de Pitágoras,
pero estudios demuestran que este ya había sido usado y entendido por otras
personas, tal vez con finalidades diferentes. Este capítulo nos muestra cómo la
matemática es implementada de diferentes maneras a través de la historia,
tomando como caso particular este famoso teorema, sus aplicaciones y el modo en
que fue entendido y demostrado por muchos El Teorema de Pitágoras es la
relación matemática que ocupa el primer lugar en el recuerdo de los tiempos
escolares. Es, sin duda alguna, la más importante, conocida, útil y popular en
casi todas las civilizaciones; la que más nombres, atención, curiosidad y
pruebas ha recibido a lo largo de los siglos.
Un examen arqueológico
realizado en el pasado siglo de las tablillas de arcilla encontradas en
Mesopotamia, pertenecientes a las civilizaciones que se desarrollaron entre los
ríos Tigris y Éufrates, ha revelado que los antiguos babilonios conocían
aspectos del teorema, más de mil años antes que el propio Pitágoras. En la
tablilla PLIMPTON 322, la cual parece un simple registro de cuentas de
operaciones comerciales, los intérpretes descubrieron una descripción empírica
de ternas pitagóricas.
Por otro lado los egipcios
para recuperar las fronteras de los lindes de las tierras, tras los periódicos
corrimientos de tierras producidos por las crecidas del río Nilo, utilizaron el
triángulo rectángulo de lados 3, 4 y 5 (o de medidas proporcionales a estos
números) para trazar una línea perpendicular a otra, a modo de "escuadra
de carpintero"; además, todas las pirámides de Egipto, excepto la de
Keops, incorporan, de alguna manera, este triángulo en su construcción. Algo
similar se puede afirmar respecto de la antigua civilización hindú y de las
antiguas culturas chinas que surgieron en las cuencas de los ríos Yangtze y
Amarillo.
Sin embargo, las
referencias históricas de dichas civilizaciones, no contiene pruebas del
teorema, por ahora sigue la creencia generalizada de que fue Pitágoras el
primero en proporcionarnos una demostración lógica de este, lo que hace justo
que haya pasado al historia con su nombre.
La
matemática griega es también conocida como matemáticas helénicas, la disciplina
practicada por esta civilización se constituye en gran heredera de los avances
hechos por Babilonia y el antiguo Egipto, sólo que desde un punto de vista
mucho más moderno y sofisticado, pues así como estas civilizaciones lograron
concebir métodos inductivos para el cálculo de diferentes cantidades, los
griegos implementaron por primera vez en el mundo el método del razonamiento
deductivo, inventando así las matemáticas abstractas, basadas en axiomas,
teoremas y definiciones, las cuales obtenían a través de la aplicación de la
lógica deductiva. Por regla general, los investigadores optan por considerar
como punto de inicio de las matemáticas helénicas a Tales de Mileto (624 a.C. –
546 a.C.) quien desarrolló importantes avances en el área geométrica, que le
permitieron calcular distancias y las dimensiones de varios objetos como las
pirámides, de las que pudo medir exactamente su altura. Así mismo, Pitágoras
(582 a.C. – 507 a.C.) Empleó los conocimientos geométricos para lograr la
resolución y demostración del teorema, que la historia terminó por ser
bautizado Teorema de Pitágoras en su honor. Igualmente, los miembros de la
escuela de este antiguo matemático, los pitagóricos lograron incluso probar que
los números irracionales existían, hecho bastante avanzado para su momento

Los griegos entre la geometría y la
aritmética
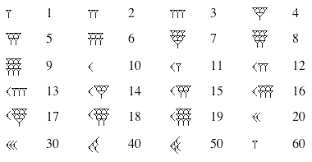
La
historia de los símbolos numerales inicia con los griegos. La geometría griega
mejora la geometría babilónica, pero en la aritmética griega, hasta donde
podemos decir los griegos dieron un gran paso atrás; no utilizaban la notación
posicional. En su lugar utilizaban símbolos específicos para múltiplos de 10 o
100. Los cálculos propiamente dichos se llevaban a cabo probablemente
utilizando un ábaco, quizá representado por guijarros en la arena,
especialmente al principio. Los griegos escribían las fracciones de varias
maneras. Una de ellas consistía en escribir el numerador, seguido por una
prima, y luego el denominador, seguido por una doble prima. A veces el
denominador se escribía dos veces. Así 21/47 se escribiría κα' μζ'' donde κα es
21 y μζ es 47. También utilizaban fracciones al estilo egipcio, y había un
símbolo especial para 1 /2. Algunos astrónomos griegos, en especial Ptolomeo,
empleaban el sistema sexagesimal babilónico por precisión, aunque utilizando
símbolos griegos para los «dígitos» componentes. Todo era muy diferente de lo
que utilizamos hoy. De hecho, era un revoltijo.
¿Qué
hubiera sucedido si los griegos no se hubiesen apartado de la notación
posicional? ¿Sería mayor su aporte a las matemáticas?
Babilonia
.
La aritmética más desarrollada en la civilización Mesopotámica fue la Acadiana.
Dos de las características más importantes de su sistema numérico fueron la
base 60 y la notación posicional. No obstante, debe señalarse que los
babilonios no usaban solamente la base 60. En ocasiones, aparecía la base 10,
pero otras bases también. Al igual que sucede con otras culturas y sistemas
numéricos, con los babilonios se dio una forma combinada de sistemas numéricos
determinados por circunstancias
históricas o incluso regionales. En lo que sí parece haber consenso es que se
dio el uso bastante sistemático de la base 60 para todos los cálculos
relacionados con la astronomía. Esto debe subrayarse:
"Tanto
el sistema sexagesimal como el sistema del valor del lugar han permanecido en
posesión permanente de la humanidad. Nuestra división presente de la hora en 60
minutos y 3 600 segundos data de los sumerios, al igual que nuestra división
del círculo en 360 grados, cada grado en 60 minutos y cada minuto en 60
segundos. Hay razón para creer que esta opción de 60 en lugar de 10 como una
unidad ocurrió en un esfuerzo por unificar sistemas de medida, aunque el hecho
de que 60 tiene muchos divisores también puede haber jugado un papel. Acerca
del sistema del valor posicional, su importancia permanente se ha comparado con
el alfabeto (ambas invenciones reemplazaron un simbolismo complejo por un
método fácilmente entendible por muchas personas). Es razonable suponer que
hindúes y griegos obtuvieron las rutas de las caravanas hacia Babilonia;
también sabemos que los académicos musulmanes lo describieron como una
invención india. La tradición babilónica, sin embargo, puede haber influido en
la aceptación tardía del sistema posicional. ‘‘(Struik, A Concise History of
Mathematics, p. 26).